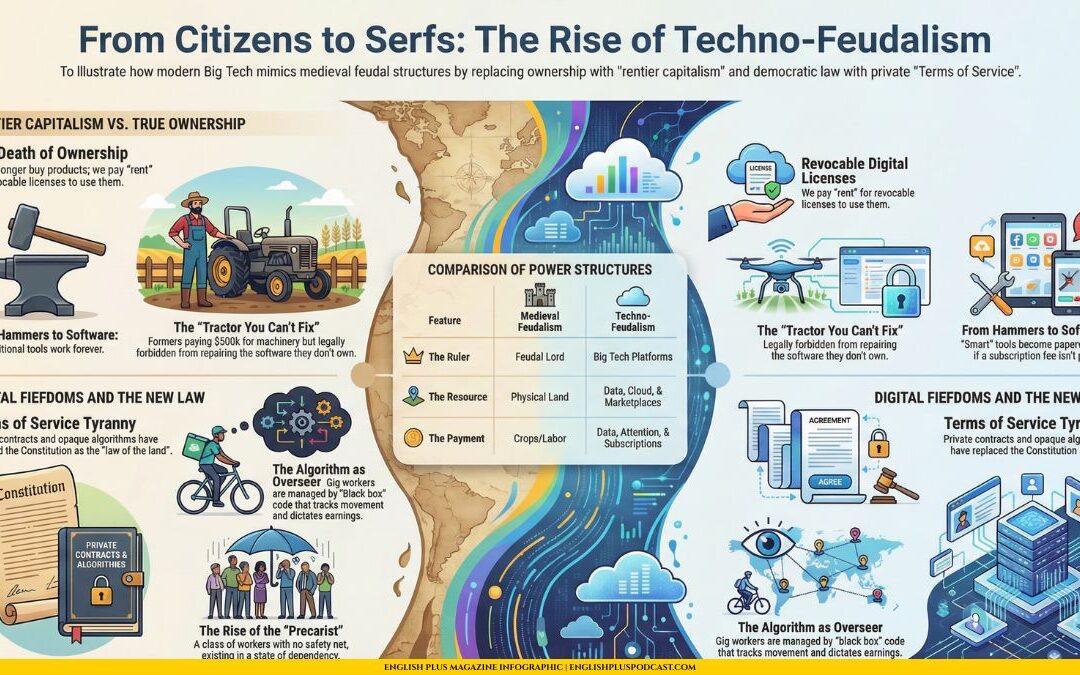
When most people think of large numbers, they might think of something like a billion, a trillion, or even a googol (a 1 followed by 100 zeros). But these numbers are minuscule compared to a number so vast, so colossal, that it defies the imagination: Graham’s Number.
Graham’s Number is so large that it cannot be written down using conventional mathematical notation. In fact, if you tried to write out the entire number, even if you used every atom in the universe as a digit, you wouldn’t come close to representing it in its entirety. It’s a number that stretches the very limits of what we can comprehend.
What Is Graham’s Number?
Graham’s Number emerged from a problem in an area of mathematics known as Ramsey theory. This branch of mathematics explores the conditions under which order must appear. Specifically, mathematician Ronald Graham was working on a problem related to hypercube connections, and he needed an upper bound to ensure a certain property would hold. The result? A number so enormous that standard mathematical notation simply couldn’t contain it.
While the exact problem that led to Graham’s Number is complex, the important takeaway is that Graham’s Number serves as a limit in this context. It’s not an exact answer to the problem but rather a bound—an upper limit beyond which the solution must lie.
The Challenge of Expressing Graham’s Number
To give you an idea of just how massive Graham’s Number is, even the exponentiation—using powers of 10—falls short. For example, a googol (10^100) is already incomprehensibly large to most people, but Graham’s Number is so much larger that trying to compare the two is futile.
Instead, mathematicians use a special notation known as “Knuth’s up-arrow notation” to express it. Here’s a simplified example:
- 3↑↑33 \uparrow\uparrow 33↑↑3 (this means 3 raised to the power of 3 raised to the power of 3).
- Now, take that result and use it as an exponent for another 3, and repeat the process a mind-boggling number of times.
Graham’s Number goes through this process many times over, and even that description is a gross understatement. The final result is a number so vast that it’s beyond the realm of what our minds can fully grasp.
The Limitations of Graham’s Number
While Graham’s Number is fascinating in its sheer size, it’s important to remember that it’s more of a theoretical concept. It’s not a number you’d encounter in everyday life, nor is it practical for solving most mathematical problems. However, it does serve as an excellent example of how mathematics can push the boundaries of what’s possible—and how even the simplest of problems can lead to astonishing results.
Interestingly, despite its enormous size, mathematicians can still make statements about the last few digits of Graham’s Number. For example, they know that the last digit of Graham’s Number is 7—a curious fact considering how large the number is.
Why Should You Care About Graham’s Number?
You might wonder why Graham’s Number matters if it’s so abstract and impractical. The truth is, while you might never use Graham’s Number in a real-world calculation, it represents the beauty and mystery of mathematics. It shows that mathematics isn’t just about solving equations or balancing checkbooks—it’s about exploring the unknown, pushing the limits of human understanding, and uncovering the infinite possibilities that numbers can represent.
A Journey Beyond the Infinite
Graham’s Number stands as a testament to the extraordinary nature of mathematics. It’s a number so immense that it challenges our very notions of size and scale, serving as a reminder that in the world of mathematics, the only limits are those of our imagination. So, while you may never need to use Graham’s Number in your day-to-day life, simply knowing it exists can inspire you to see mathematics in a new light—a field full of wonder, mystery, and endless possibilities.
Expand Your Vocabulary
- Graham’s Number: A mathematical concept so large that it cannot be expressed in conventional notation. In everyday use, when you want to describe something unimaginably vast or complex, you might compare it to “Graham’s Number.” For example, “The amount of work left to do feels like Graham’s Number!”
- Conventional Notation: A standard way of writing numbers or symbols. In daily life, this could refer to common ways of expressing things. For instance, “We need to follow conventional notation when writing scientific reports.”
- Exponentiation: The process of raising a number to the power of another number, like squaring or cubing. In everyday contexts, you might use this concept when discussing growth, such as “The population is growing exponentially.”
- Ramsey Theory: A branch of mathematics focused on finding order in chaos. Though it’s specific to math, you can use the idea of finding order in unexpected places in conversations. For example, “Sometimes, life feels chaotic, but like Ramsey theory, there’s order beneath the surface.”
- Upper Bound: A limit that something cannot exceed. You might use this term when discussing maximum limits in life, such as “I’ve reached my upper bound for stress this week.”
- Hypercube: A generalization of a 3-dimensional cube to higher dimensions. In a more abstract sense, you could use it to describe complex, multi-dimensional problems in life, like “Planning this event feels like dealing with a hypercube of logistics.”
- Theoretical: Something that exists in thought or as an idea but may not be practical. You might say, “While it’s theoretical, this idea could change how we approach the project.”
- Abstract: A concept that is not tied to physical reality or concrete examples. In everyday language, it might refer to an idea that is hard to grasp. For example, “Her explanation was too abstract for me to follow.”
- Impractical: Not useful or realistic for everyday situations. You might say, “His suggestion was brilliant but completely impractical for our current situation.”
- Incomprehensible: Something that is impossible to understand. For instance, you could describe a confusing situation by saying, “The instructions were completely incomprehensible.”
Let’s Talk
- How does the concept of numbers as vast as Graham’s Number challenge your understanding of mathematics? Can you think of other examples in life where our understanding is limited by scale?
- Do you find it fascinating or overwhelming that mathematics can produce such enormous numbers? How might this relate to the complexity of other fields, like science or philosophy?
- In your own life, have you ever encountered a situation that felt as vast or incomprehensible as Graham’s Number? How did you handle it?
- Considering that Graham’s Number is more theoretical than practical, can you think of any ideas or concepts in your daily life that might be brilliant in theory but challenging to apply in practice?
- How might the idea of finding order in chaos, as seen in Ramsey theory, relate to challenges you face in your personal or professional life? Can you think of a time when you found unexpected order in a chaotic situation?
- If you could create a real-world analogy for a hypercube, what complex, multi-dimensional problem in your life would it represent? How might you go about solving it?
- Do you believe that some ideas are too abstract or theoretical to be useful in everyday life, or do you think that even the most complex concepts can have practical applications? Why?
- How do you deal with situations or instructions that seem incomprehensible? What strategies help you make sense of them?
- Is there a point where reaching an ‘upper bound’ becomes a positive challenge rather than a limitation? How can you turn limits into opportunities?
- When faced with something impractical, how do you balance creativity and reality to find a workable solution? Can you share an example?








0 Comments